多項式的概率檢查

要做多項式的概率檢查，需要有兩個多項式，而且同為兩個次數不多於d的多項式。驗證者只要進行一次多項式隨機挑戰就可以。這就是Schwartz-Zippel定理。
因為可以進一步地去使用多項式承諾(Polynomial Commitment)，讓證明者負責計算x在某一任意地方的值，然後發送證明，這樣驗證者的工作量可以減少。
假設要驗證向量a + 向量b是否等於向量c:
可以先把向量編碼成多項式(系數編碼方式)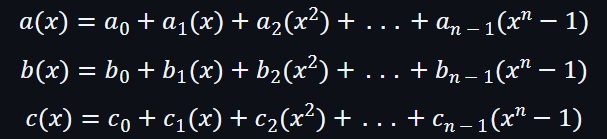

驗證者只需要給出一個隨機挑戰值(任意值) ζ∈F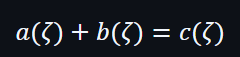

如果成功證明到以上公式，則向量a + 向量b是等於向量c。
不過當要驗證向量a乘向量b是否等於向量c，就需要用拉格朗日插值的編碼方式，經轉換之後如下: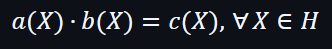

但在這公式，驗證者需要挑戰多次才可以縮小出錯概率。
因此，需要更高效的方法來進行檢測，目標是只用一次就可以檢查出Prover是否存在作弊行為。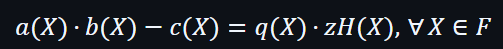

在公式上可以看到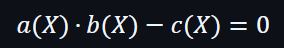

所以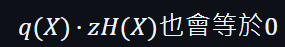

換言之，在X∈H的條件下: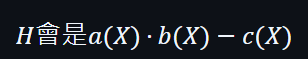

的根集合。因為X必須要使到: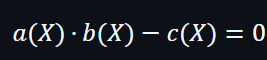

另外，a(X)⋅b(X)−c(X)可以被多項式zH(X)整除，並得到一個商多項式q(X)。所以只要讓證明者計算出q(X)，就可以使到驗證者的工作量減少至只需進行一次隨機檢測就可知道a(X)⋅b(X)−c(X)在X∈H的條件下是否等於0。而驗證者計算 zH(ζ) 需要 O(n) 的計算量。